Gustavo Gutierrez 4D
SÓLIDOS GEOMÉTRICOS - MATE 2
ARTÍCULOS DE GEOMETRÍA DEL ESPACIO, JUEGOS DE INGENIO Y DEMÁS TEMAS RELACIONADOS A LAS MATEMÁTICAS
29 nov 2010
Volumen
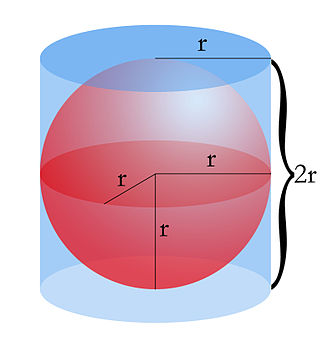
El Volumen de una esfera es dos tercios del volumen del cilindro circunscrito a la esfera cuya base es igual al círculo del diámetro de la circunferencia del cilindro. Entonces:

es decir, el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).
el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).


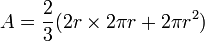
2r×2πr es el lado del cilindro, es un rectángulo con base 2πr y altura de 2r. 2πr² es el área de las dos bases circulares. Al sumar todas las áreas nos da el total de la esfera (mirar imagen).



Es más fácil recordarla al saber el volumen, ya que el área es igual a la derivada de este.
alison montoya
El Volumen de una esfera es dos tercios del volumen del cilindro circunscrito a la esfera cuya base es igual al círculo del diámetro de la circunferencia del cilindro. Entonces:

es decir,
 el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).
el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).

[editar] Área
Arquímides dijo que la superficie de la esfera era también de dos tercios respecto al cilindro, entonces: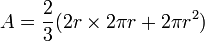
2r×2πr es el lado del cilindro, es un rectángulo con base 2πr y altura de 2r. 2πr² es el área de las dos bases circulares. Al sumar todas las áreas nos da el total de la esfera (mirar imagen).



Es más fácil recordarla al saber el volumen, ya que el área es igual a la derivada de este.
28 nov 2010
CONO TRUNCADO
CONO TRUNCADO
El cono truncado o tronco de cono es el cuerpo geométrico que resulta al cortar un cono por un plano paralelo a la base y separar la parte que contiene al vértice.
Elementos del cono truncado

- La sección determinada por al corte es la base menor.
- La altura es el segmento que une perpendicularmente las dos bases
- Los radios son los radios de sus bases.
- La generatriz es el segmento que une dos puntos del borde de las dos bases.
Obtenemos la generatriz del cono truncado aplicando el teorema de Pitágoras en el triángulo sombreado:
ÁREA LATERAL DE UN CONO TRUNCADO

ÁREA DE UN CONO TRUNCADO

VOLUMEN DE UN CONO TRUNCADO

JOHANNA CRUZ
24 nov 2010
CONO
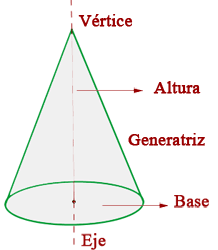
El cono es el cuerpo de revolución que se obtiene al girar un triángulo rectángulo sobre uno de sus catetos.
Elementos del cono
Es el cateto fijo alrededor del cual gira el triángulo.
Base
Es el círculo que forma el otro cateto.
Altura
Es la distancia del vértice a la base.
Generatriz
Es la hipotenusa del triángulo rectángulo.
Por el teorema de Pitágoras la generatriz del cono será igual a:

Área lateral de un cono
Área de un cono
Volumen de un cono
14 nov 2010
El término poliedro es el que se utiliza para designar a aquellas figuras geométricas tridimensionales que están compuestas por varias caras o facetas. Se puede decir que el poliedro es el equivalente de los polígonos, las figuras geométricas planas con muchos lados pero sin tridimensionalidad. El nombre de poliedro proviene del idioma griego para el cual poli significa “muchos” y edro o edron quiere decir “caras”.
Los poliedros son mucho más llamativos en términos visuales que un polígono. Esto tiene que ver con el hecho de que ganan tridimensionalidad y, por tanto, su superficie se vuelve mucho más compleja. Los elementos que normalmente componen a un poliedro son tres, algunos de ellos equivalentes a los del polígono: las caras, las aristas y los vértices. Las caras son los planos que se forman a lo largo de la superficie del poliedro y que pueden ser muy numerosas dependiendo del poliedro que se trate. Luego prosiguen las aristas o líneas que delimitan los planos entre sí y que pueden ser compartidas por dos planos de manera conjunta. Finalmente, los vértices, al igual que en el polígono, son el punto de unión de dos o más aristas así como también de dos o más planos.
Los poliedros, como es de suponerse, son figuras complejas que pueden ser agrupadas en dos conjuntos principales: los poliedros regulares y los irregulares. Mientras que los primeros se caracterizan por estar compuestos por caras y vértices iguales entre sí, los irregulares son una composición de caras y vértices de diferente tamaño y nivel, por lo cual su vista final es mucho más impresionante y desordenada. Entre los primeros, los poliedros regulares, encontramos por ejemplo a los cubos. En el grupo de poliedros irregulares una de las formas más conocidas es el prisma en todas sus variantes así como también las figuras que llevan el nombre de “truncado” junto al número de caras que poseen (por ejemplo el Tetraedro truncado).
Diego Carrasco
Los poliedros son mucho más llamativos en términos visuales que un polígono. Esto tiene que ver con el hecho de que ganan tridimensionalidad y, por tanto, su superficie se vuelve mucho más compleja. Los elementos que normalmente componen a un poliedro son tres, algunos de ellos equivalentes a los del polígono: las caras, las aristas y los vértices. Las caras son los planos que se forman a lo largo de la superficie del poliedro y que pueden ser muy numerosas dependiendo del poliedro que se trate. Luego prosiguen las aristas o líneas que delimitan los planos entre sí y que pueden ser compartidas por dos planos de manera conjunta. Finalmente, los vértices, al igual que en el polígono, son el punto de unión de dos o más aristas así como también de dos o más planos.
Los poliedros, como es de suponerse, son figuras complejas que pueden ser agrupadas en dos conjuntos principales: los poliedros regulares y los irregulares. Mientras que los primeros se caracterizan por estar compuestos por caras y vértices iguales entre sí, los irregulares son una composición de caras y vértices de diferente tamaño y nivel, por lo cual su vista final es mucho más impresionante y desordenada. Entre los primeros, los poliedros regulares, encontramos por ejemplo a los cubos. En el grupo de poliedros irregulares una de las formas más conocidas es el prisma en todas sus variantes así como también las figuras que llevan el nombre de “truncado” junto al número de caras que poseen (por ejemplo el Tetraedro truncado).
Diego Carrasco
12 nov 2010
Construcción de sólidos geométricos
Cubo:
1.- Se trazan cuatro (4) cuadrados iguales, uno seguido del otro.
2.- Luego se dibujan dos (2) cuadrados más a cada lado de uno de los que hiciste anteriormente.
3.- Recuerda que se deben trazar sus respectivas pestañas para así lograr pegar todo el cuerpo geométrico y formar la figura.
Nota: La longitud de los cuadrados debe ser de igual medida en todos los cuadrados.
Cono:
1.- Se traza un círculo que será la base.
2.- Luego se dibuja un triángulo cuya base debe ser en forma de arco.
3.- Las pestañas debes hacerlas en la base del triángulo.
Pirámide Triangular:
1.- Se trazan tres (3) triángulos iguales, uno a continuación del otro.
2.- Luego se dibuja otro triángulo más pequeño, que servirá como base debajo de alguno de los trazados anteriormente.
3.- Recuerda dibujar las pestañas.
GUSTAVO GUTIERREZ 4D
9 nov 2010
Solidos de Arquimedes
CUBOCTAEDRO
Caras: 14
Caras: 14
Aristas: 24
Vértices: 12
ICOSIDODECAEDRO
Caras :32
Aristas :60
Vértices:30
TETRAEDRO TRUNCADO
Caras: 8
Aristas: 18
Vértices : 12
OCTAEDRO TRUNCADO
Caras: 14
Aristas: 36
Vértices: 24
GUSTAVO GUTIERREZ
Suscribirse a:
Entradas (Atom)