SÓLIDOS GEOMÉTRICOS

29 nov 2010

Volumen
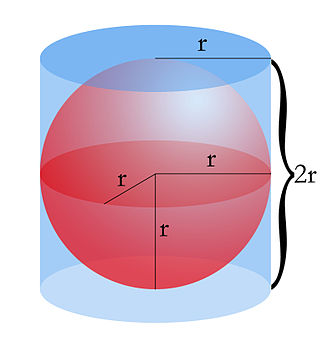
El Volumen de una esfera es dos tercios del volumen del cilindro circunscrito a la esfera cuya base es igual al círculo del diámetro de la circunferencia del cilindro. Entonces:
$V = \frac{2}{3} \times \pi r^2 \times 2r$
es decir, $\frac{2}{3}$ el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).
$V = \frac{2}{3} \times 2\pi r^3$
$V = \frac{4\pi r^3}{3}$

[editar] Área

Arquímides dijo que la superficie de la esfera era también de dos tercios respecto al cilindro, entonces: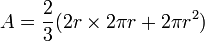
$A = \frac{2}{3} (2r \times 2\pi r + 2\pi r^2)$
2r×2πr es el lado del cilindro, es un rectángulo con base 2πr y altura de 2r. 2πr² es el área de las dos bases circulares. Al sumar todas las áreas nos da el total de la esfera (mirar imagen).
$A = \frac{2}{3} (4\pi r^2 + 2\pi r^2)$
$A = \frac{2}{3} (6\pi r^2)$
$\ A = 4\pi r^2$
Es más fácil recordarla al saber el volumen, ya que el área es igual a la derivada de este.

alison montoya

SÓLIDOS GEOMÉTRICOS - MATE 2

29 nov 2010

[editar] Área

No hay comentarios:

Publicar un comentario