Gustavo Gutierrez 4D
ARTÍCULOS DE GEOMETRÍA DEL ESPACIO, JUEGOS DE INGENIO Y DEMÁS TEMAS RELACIONADOS A LAS MATEMÁTICAS
29 nov 2010
Volumen
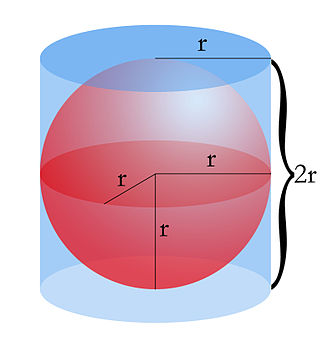
El Volumen de una esfera es dos tercios del volumen del cilindro circunscrito a la esfera cuya base es igual al círculo del diámetro de la circunferencia del cilindro. Entonces:

es decir, el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).
el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).


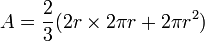
2r×2πr es el lado del cilindro, es un rectángulo con base 2πr y altura de 2r. 2πr² es el área de las dos bases circulares. Al sumar todas las áreas nos da el total de la esfera (mirar imagen).



Es más fácil recordarla al saber el volumen, ya que el área es igual a la derivada de este.
alison montoya
El Volumen de una esfera es dos tercios del volumen del cilindro circunscrito a la esfera cuya base es igual al círculo del diámetro de la circunferencia del cilindro. Entonces:

es decir,
 el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).
el área de la base del cilindro por su altura más cuatro veces su tamaño inicial respecto al de una esfera la mitad de su tamaño posterior(mirar imagen).

[editar] Área
Arquímides dijo que la superficie de la esfera era también de dos tercios respecto al cilindro, entonces: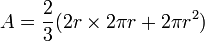
2r×2πr es el lado del cilindro, es un rectángulo con base 2πr y altura de 2r. 2πr² es el área de las dos bases circulares. Al sumar todas las áreas nos da el total de la esfera (mirar imagen).



Es más fácil recordarla al saber el volumen, ya que el área es igual a la derivada de este.
28 nov 2010
CONO TRUNCADO
CONO TRUNCADO
El cono truncado o tronco de cono es el cuerpo geométrico que resulta al cortar un cono por un plano paralelo a la base y separar la parte que contiene al vértice.
Elementos del cono truncado

- La sección determinada por al corte es la base menor.
- La altura es el segmento que une perpendicularmente las dos bases
- Los radios son los radios de sus bases.
- La generatriz es el segmento que une dos puntos del borde de las dos bases.
Obtenemos la generatriz del cono truncado aplicando el teorema de Pitágoras en el triángulo sombreado:
ÁREA LATERAL DE UN CONO TRUNCADO

ÁREA DE UN CONO TRUNCADO

VOLUMEN DE UN CONO TRUNCADO

JOHANNA CRUZ
24 nov 2010
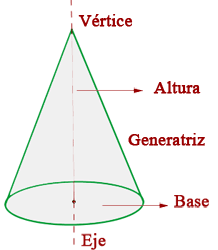
CONO
El cono es el cuerpo de revolución que se obtiene al girar un triángulo rectángulo sobre uno de sus catetos.
Elementos del cono
Es el cateto fijo alrededor del cual gira el triángulo.
Base
Es el círculo que forma el otro cateto.
Altura
Es la distancia del vértice a la base.
Generatriz
Es la hipotenusa del triángulo rectángulo.
Por el teorema de Pitágoras la generatriz del cono será igual a:

Área lateral de un cono
Área de un cono
Volumen de un cono
14 nov 2010
El término poliedro es el que se utiliza para designar a aquellas figuras geométricas tridimensionales que están compuestas por varias caras o facetas. Se puede decir que el poliedro es el equivalente de los polígonos, las figuras geométricas planas con muchos lados pero sin tridimensionalidad. El nombre de poliedro proviene del idioma griego para el cual poli significa “muchos” y edro o edron quiere decir “caras”.
Los poliedros son mucho más llamativos en términos visuales que un polígono. Esto tiene que ver con el hecho de que ganan tridimensionalidad y, por tanto, su superficie se vuelve mucho más compleja. Los elementos que normalmente componen a un poliedro son tres, algunos de ellos equivalentes a los del polígono: las caras, las aristas y los vértices. Las caras son los planos que se forman a lo largo de la superficie del poliedro y que pueden ser muy numerosas dependiendo del poliedro que se trate. Luego prosiguen las aristas o líneas que delimitan los planos entre sí y que pueden ser compartidas por dos planos de manera conjunta. Finalmente, los vértices, al igual que en el polígono, son el punto de unión de dos o más aristas así como también de dos o más planos.
Los poliedros, como es de suponerse, son figuras complejas que pueden ser agrupadas en dos conjuntos principales: los poliedros regulares y los irregulares. Mientras que los primeros se caracterizan por estar compuestos por caras y vértices iguales entre sí, los irregulares son una composición de caras y vértices de diferente tamaño y nivel, por lo cual su vista final es mucho más impresionante y desordenada. Entre los primeros, los poliedros regulares, encontramos por ejemplo a los cubos. En el grupo de poliedros irregulares una de las formas más conocidas es el prisma en todas sus variantes así como también las figuras que llevan el nombre de “truncado” junto al número de caras que poseen (por ejemplo el Tetraedro truncado).
Diego Carrasco
Los poliedros son mucho más llamativos en términos visuales que un polígono. Esto tiene que ver con el hecho de que ganan tridimensionalidad y, por tanto, su superficie se vuelve mucho más compleja. Los elementos que normalmente componen a un poliedro son tres, algunos de ellos equivalentes a los del polígono: las caras, las aristas y los vértices. Las caras son los planos que se forman a lo largo de la superficie del poliedro y que pueden ser muy numerosas dependiendo del poliedro que se trate. Luego prosiguen las aristas o líneas que delimitan los planos entre sí y que pueden ser compartidas por dos planos de manera conjunta. Finalmente, los vértices, al igual que en el polígono, son el punto de unión de dos o más aristas así como también de dos o más planos.
Los poliedros, como es de suponerse, son figuras complejas que pueden ser agrupadas en dos conjuntos principales: los poliedros regulares y los irregulares. Mientras que los primeros se caracterizan por estar compuestos por caras y vértices iguales entre sí, los irregulares son una composición de caras y vértices de diferente tamaño y nivel, por lo cual su vista final es mucho más impresionante y desordenada. Entre los primeros, los poliedros regulares, encontramos por ejemplo a los cubos. En el grupo de poliedros irregulares una de las formas más conocidas es el prisma en todas sus variantes así como también las figuras que llevan el nombre de “truncado” junto al número de caras que poseen (por ejemplo el Tetraedro truncado).
Diego Carrasco
12 nov 2010
Construcción de sólidos geométricos
Cubo:
1.- Se trazan cuatro (4) cuadrados iguales, uno seguido del otro.
2.- Luego se dibujan dos (2) cuadrados más a cada lado de uno de los que hiciste anteriormente.
3.- Recuerda que se deben trazar sus respectivas pestañas para así lograr pegar todo el cuerpo geométrico y formar la figura.
Nota: La longitud de los cuadrados debe ser de igual medida en todos los cuadrados.
Cono:
1.- Se traza un círculo que será la base.
2.- Luego se dibuja un triángulo cuya base debe ser en forma de arco.
3.- Las pestañas debes hacerlas en la base del triángulo.
Pirámide Triangular:
1.- Se trazan tres (3) triángulos iguales, uno a continuación del otro.
2.- Luego se dibuja otro triángulo más pequeño, que servirá como base debajo de alguno de los trazados anteriormente.
3.- Recuerda dibujar las pestañas.
GUSTAVO GUTIERREZ 4D
9 nov 2010
Solidos de Arquimedes
CUBOCTAEDRO
Caras: 14
Caras: 14
Aristas: 24
Vértices: 12
ICOSIDODECAEDRO
Caras :32
Aristas :60
Vértices:30
TETRAEDRO TRUNCADO
Caras: 8
Aristas: 18
Vértices : 12
OCTAEDRO TRUNCADO
Caras: 14
Aristas: 36
Vértices: 24
GUSTAVO GUTIERREZ
5 nov 2010
Biografía de Paolo Ruffini
Estudió matemáticas, literatura, filosofía, medicina y biología en la Universidad de Módena. Fue médico y matemático
Después de graduarse fue nombrado en 1788 profesor de Fundamentos de Análisis y de Elementos Matemáticos en la universidad de Módena, de la cual fue nombrado rector en 1814.En 1791 obtuvo permiso para impartir clases de clínica médica en la misma Universidad
Después de ocupar las tropas de Napoleón la ciudad de Módena, fue nombrado, en 1796, representante del Departamento de Paramo en el Consejo de la República Cisalpina creada por Napoleón. Dos años después reanudó sus actividades científicas y al negarse a pronunciar el juramento de fidelidad a la República Cisalpina fue apartado de sus actividades docentes y cargos públicos.
En 1799 al entrar los austriacos en Módena le fueron devueltas sus cátedras. En 1806 pasó a enseñar matemáticas aplicadas en la Escuela Militar.
Durante 1817-1818 estudió la enfermedad del tifus al declararse una epidemia.
Perteneció a las más doctas corporaciones de la Italia de su tiempo y llegó a ser Presidente del Instituto Italiano de las Ciencias.
Fue calificado como el matemático más
- Fue admirador de Lagrange
- Ocupo la Cátedra de Análisis que dejó vacante Cassiani
- Heinrich Burkhardt realizó un completo estudio del trabajo de Ruffini con relación a la teoría de grupos de sustitución y fue publicada en 1892 bajo el titulo: "Die Anfauge des Gruppentheorie und Paolo Ruffini"
- En sus escritos aparece la nueva idea de "grupo" que llamaba permutaciones
- Fue el primero en afirmar que las ecuaciones de quinto grado no pueden resolverse por radicales
- Mientras era estudiante, sustituyó a su profesor de fundamentos de análisis.
- El único matemático de su época que se interesó por su trabajo fue Cauchy, que era bastante descortés con sus colegas.
Lilian Paiva Castillo
3 nov 2010
Biografia de Euler
Leonhard Euler fue un respetado matemático y físico. Nació el 15 de abril de 1707 en Basilea y murió el 18 de septiembre de 1783 en San Petersburgo .Se lo considera el principal matemático del siglo XVIII y como uno de los más grandes de todos los tiempos.
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática. Asimismo se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Euler ha sido uno de los matemáticos más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes.Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros.»En conmemoración suya, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos, así como en numerosos sellos postales tanto suizos como alemanes y rusos. El asteroide (2002) Euler recibió ese nombre en su honor.
Gustavo Gutierrez
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática. Asimismo se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Euler ha sido uno de los matemáticos más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes.Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros.»En conmemoración suya, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos, así como en numerosos sellos postales tanto suizos como alemanes y rusos. El asteroide (2002) Euler recibió ese nombre en su honor.
Gustavo Gutierrez
29 oct 2010
la pelota de futbol
http://www.youtube.com/watch?v=W8IPuZKes58ç < ---- aqui esta la pagina

en este video se muestra mejor la forma de una pelota de futbol -
alison montoya

en este video se muestra mejor la forma de una pelota de futbol -
alison montoya
CUBO DE RUBIK
El cubo de Rubik (o cubo mágico, como se conoce en algunos países) es un rompecabezas mecánico inventado por el escultor y profesor de arquitectura húngaro Ernö Rubik en 1974. Se trata de un conocido rompecabezas cuyas caras están divididas en cuadrados de un mismo color que se pueden cambiar de posición. El objetivo de resolver el rompecabezas se consigue al colocar todos los cuadrados de cada cara del cubo con el mismo color.
Requiere 20 movimientos para ser resuelto (SOLUCIÓN).
JOHANNA CRUZ SOLANO
POLIEDROS EN LA CIENCIA Y NATURALEZA
- En 1.996 se concedió el premio Nobel de Química a tres investigadores por el descubrimiento del fullereno( C60 ) cuya forma es un icosaedro truncado.
- Los panales de abejas tienen forma de prismas hexagonales.
- El virus de la poliomielitis y de la verruga tienen forma de Icosaedro.
- Las células del tejido epitelial tienen forma de Cubos y Prismas.

JOHANNA CRUZ SOLANO
ORIGAMI MODULAR
El Origami Modular o Papiroflexia Modular es una técnica de doblado de papel que consiste en crear estructuras complejas partiendo de muchos trozos iguales de papel; con el objetivo de construir sólidos platónicos y observar sus propiedades.
A continuación las imágenes de varios sólidos geométricos:
A continuación las imágenes de varios sólidos geométricos:
 |
| FIGURAS USANDO EL MÓDULO DE SONOBE |
 |
| Pentaquisdodecaedro Estrellado (60 módulos de Sonobe) |
 |
| ICOSAEDRO ESTRELLADO |
JOHANNA CRUZ SOLANO
28 oct 2010
POLIEDROS REGULARES
Los poliedros regulares son poliedros convexos con todas las caras idénticas que son polígonos regulares y con todos los vértices recibiendo el mismo número de aristas. Solo existen 5 tipos de poliedros regulares: tetraedro, octaedro, icosaedro, cubo y dodecaedro.
¿Por qué hay sólo 5 tipos de poliedros regulares?
En un vertice pueden 3,4 o 5 triángulos equiláteros, 3 cuadrados o 3 pentagonos, con 3 hexagonos se aplanarían.
DIEGO CARRASCO
27 oct 2010
POLIEDROS EN LA VIDA COTIDIANA
ICOSAEDRO TRUNCADO
El icosaedro truncado es un sólido de Arquímedes que se obtiene truncando cada vértice de un icosaedro.
Y ahora te preguntaras: COMÓ ES y en DONDÉ LO VEO COTIDIANAMENTE?
Pues lo ves todos los recreos, cuando te sientas a ver a tus equipos de futbol, cuando fue el mundial & en todos lados.
Pues bien hablo de la pelota y se llama asi dado que los gajos de cuero que la formaban eran hexágonos y pentágonos dispuestos en forma de icosaedro truncado. Al ser inflada la pelota tomaba la forma esférica característica.
Icosaedro Truncado | |
|---|---|
Grupo | |
Número de caras | 32 |
Polígonos que forman las caras | |
Número de aristas | 90 |
Número de vértices | 60 |
Tipo de Vértice | Uniforme de Orden 3 |
Caras relacionadas en los vértices | |
Simetría | Icosaédrica (Ih) |
Propiedades | Poliedro convexo, de vértices uniformes |
STEPHANIA GÓMEZ
CRITERIOS DE CLASIFICACIÓN DE LOS POLIEDROS
Los poliedros pueden ser clasificados en muchos grupos según la familia de donde provienen o de las características que los diferencian; según sus características, se distinguen:
- Convexos, como el cubo, o el tetraedro, cuando cualquier par de puntos del espacio que estén dentro del cuerpo los une un segmento de recta también interno. En el caso de que dicho seg se salga del cuerpo se dice que son poliedros cóncavos
- Poliedro de caras regulares, cuando todas las caras del poliedro son polígonos regulares.
- Poliedro de caras uniformes, cuando todas las caras son iguales.
- Se dice poliedro de aristas uniformes cuando en todas sus aristas se reúnen el mismo número de caras.
- Se dice poliedro de vértices uniformes cuando en todos los vértices del poliedro convergen el mismo número de caras y en el mismo orden.
- Se dice poliedro regular o regular y uniforme, como el tetraedro o el icosaedro, cuando es de caras regulares, de caras uniformes de vértices uniformes y de aristas uniformes.
- Estos grupos no son excluyentes entre sí; es decir, un poliedro puede estar incluido en más de uno de ellos.
Gustavo Gutiérrez
DEFINICIÓN DE UN POLIEDRO
Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito.
Gustavo Gutiérrez
Suscribirse a:
Comentarios (Atom)